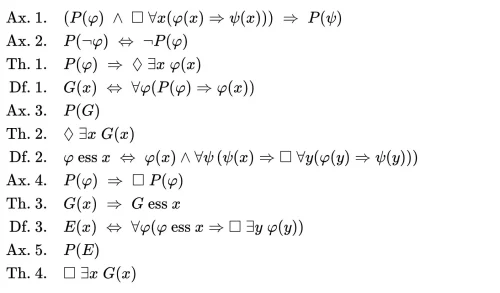بعضی از ریاضیدانها مترصد این بودند که با استفاده از منطق به اثبات خدا بپردازند. و در این یادداشت، آنچیزی را که کشف کردهاند باهم مرور میکنیم.
چه کسی نخستینبار دربارهی خدا به عنوان جستاری ریاضیاتی اندیشید؟ نگران نباشید. هنوز این بحث را قویاً تعدادی از دانشمندان نخبه به عنوان اساس کارشان پی گرفتهاند.
اما پرسش این است که آیا میتوان اثبات خدا را با ریاضیات فرمولبندی کرد؟ در حقیقت، در گذر قرنها، چند ریاضیدان بارها کوشیدهاند وجود امر قدسی را اثبات نمایند. از پاسکال گرفته تا دکارت و لایبنیتس و گودل که در اینباره قلمها فرسودهاند! (دربارهی این موضوع نیز حوالی سال 1987 مطلبی چاپ شده بود).
بیشتر بخوانید: گذر درهمتنیدگی کوانتومی از فلسفه تا فیزیک ؛ آیا انیشتین اشتباه میکرد؟
اثبات خدا با منطق و ریاضیات
احتمالاً، شگفتترین چیز این باشد که در پیشنویسی که نخستین بار در سال 2013 منتشر شد الگوریتمی اثبات زنجیره استدلالهای منطقی گودل را سنجید و در نهایت به این نتیجه رسید که بیشک اثبات او درست است. بنابراین شاید از خودتان بپرسید که در نهایت، ریاضیات تمام استدلالهای خداناباوران را رد میکند؟
همانطور که احتمالاً حدس زدهاید، خیر اینطور نیست. گودل ضرورتاً اثبات کرد چیزی وجود دارد که او آن را «الوهیت (امر قدسی)» نامیده است، که ضرورتاً پیآمد مفروضاتی قطعی بود. اما اینکه آیا این مفروضات دقیق هستند یا نه میتواند محلی از تردید باشد.
برای مثال، اگر من فرض کنم که همهی گربهها سه رنگاند و بدانم که تمام گربههای سهرنگی همیشه ماده هستند، سپس میتوانم نتیجه بگیرم: تقریباً تمامی گربهها ماده هستند. حتّی اگر این استدلال منطقی صحیح باشد این فرض صادق نیست.
چرا که این فرض که همهی گربهها سهرنگ هستند، کذب است. اگر یکی بخواهد دربارهی هستومندهای مشاهدهپذیر در محیط، نظیر گربهها اظهاراتی بکند میتواند با تحقیقات علمی آن را بسنجد. امّا اگر دربارهی اثبات یک وجود قدسی بخواهیم بگوییم مسئله کمی پیچیدهتر است.
پاسکال راه متفاوتی برای اثبات خدا در پی گرفت؟
لایبنیتس، دکارت و گودل بر اثباتهای هستیشناسانهی وجود خدا تکیه کرده بودند تا بر این اساس وجود امر قدسی را از یکسری احتمالات منطقی استنتاج کنند، اما در این میان، پاسکال رهیافت متفاوتتری را به کار بست: اگر بخواهیم از نقطه نظر امروزی به تحلیل او نگاهی در اندازیم میتوانیم یککمکی شبیه به نظریهی بازیها بدانیمش، امّا خوب در این مورد، ما آن را شرطبندی پاسکال مینامیم.
برای انجام این رویکرد، او دو احتمال را تدارک میبیند. نخست، خدا وجود دارد. و دوم، خدا وجود ندارد. سپس او نتایج و پیآمدهای باور داشتن و یا نداشتن به خدا را بعد از مرگ میسنجد. اگر اینجا یک موجود قدسی وجود داشته باشد و کسی به آن باور داشته باشد در نهایت به بهشت میرسد؛ و در غیر این صورت، به جهنم خواهد رفت. و حتی در دیگر سو، اگر خدا وجود هم نداشته باشد هیچ اتفاقی نمیفتد، آن هم صرف نظر از اینکه مذهبی باشید یا نه.
بنابراین، بهترین استراتژی نزد پاسکال اعتقاد به خداست. چرا که در نهایت شما را به بهشت میرساند. و در بدترین سناریو هم هیچاتفاقی نمیفتد. اما در بدترین سناریو اگر شما باور نداشته باشید کارتان در جهنم تمام خواهد شد!
اندیشههای پاسکال همه فهماند اما به نوشتههای مذهبیون ارجاع میدهد و دربارهی اثبات یک موجود فراطببیعی چیزی به دست نمیدهد. در واقع امر، آنها فقط میگویند که به باوری که بر پایهی فرصتطلبی است محلق شوید! ــمیدانید؟
از آنسلم تا دکارت؛ چه میگفتند؟
رهیافتهای هستیشناسانه با طبیعت کنجکاوانهی انسانی همدلترند حتی اگر تغییراتی هم در ذهن خداناباوران ایجاد نکند! مثلاً آنسِلم کانتِربِری خداشناس و فیلسوف قرن 12 میلادی که ایدههایش را در پایان هزارهی پیشین بیان کرده، گفته است که:
خدا را به عنوان وجودی فراتر از هر اندیشهای در نظر میگیرد. و در وهلهی بعد میافزاید که اگر خدایی وجود نداشته باشد، سپس کسی خواهد توانست چیزی عظیمتر از آن را تصوّر بکند: به عبارتی، موجودی که فراتر از ان نتوان تصور کرد. امّا چیزی شبیه به خدا، این وجودی که هم هست و هم منتهیالیه کمال و نیکیست. این، البته فرض بیهودهای است. چرا که هیچچیز نمیتواند بزرگتر از بزرگترین چیز قابل تصور باشد. بر این اساس، این فرض که خدا وجود ندارد باید غلط باشد.
لایبنیتس معادلهی اثبات خدا را بههم زد!
چند سده وقت لازم بود که برگشتی دوباره به ایدهی هستیشناسانه اثبات خدا داشته باشیم که آن هم کسی نبود به به جز رنه دکارت که بیشک ناآشنا با نوشتههای آنسلم نبوده است. او بخش مهمی از بحثهای وجودی را برای وجود قدسی به عنوان موجودی کمالیافته به پیش کشیده بود.
لایبنیتس نیز دههها بعد روی آن کار کرد و نقصانهای این دیدگاه را در یافت: «او معتقد بود که دکارت، نشان نداده بود که «ویژگیهای تعالیبخش» هستومندهای خاص، از تثلیث گرفته تا خدا با کمالگرایی سازگار هستند یا خیر».
لایبنیتس مترصد بود که بگوید کمالگرایی نمیتواند ویژگی مشاهدهپذیری باشد. از دیگر سو، نمیتوان آن را نفی کرد که ویژگی کمال در یک موجود واحد گرد هم میآید یا خیر. بدین ترتیب، احتمال وجود یک موجود قدسی باید واقعی باشد. بنابر آنچه که بحثهای آنسلم و دکارت به میان میکشند، ضرورتاً خدا وجود دارد.
گودل چگونه به اثبات خدا میپردازد؟
به هر روی، از نقطه نظر ریاضیات، این آزمایشات فکری تنها با آرای گودل واقعاً جدی گرفته شدند. این خیلی شگفتآور نیست: این دانشمند نیز پیشتر در سن 25 سالگیاش، با نشان دادن اینکه ریاضیات همیشه حاوی گزارههای صادق است که نمیتوان آنها را اثبات کرد، موضوع را تغییر داده بود و برای اثبات چنین چیزی نیز از منطق بهره جسته بود. که همین منطق هم او را قادر ساخت تا وجود خدا را اثبات کند. به این 12 مرحله که مجموعهای از اصولات (Ax)، نظریهها (Th) و تعاریف (Df) است بنگرید:
گزارههای منطقی گودل آنقدر ها هم مرموز نیست!
اجمالاً، این عبارات منطقی، شاید تا حدّی مرموز به نظر برسند امّا بیایید قدم به قدم ایدهی گودل را پی بگیریم. او با یک اصلــیکفرض آغاز میکند، به عبارت دیگر: اگر φ دارایی P باشد و همیشه به دنبال φ ، یک ψ بیاید، همچنین ψ عضوی از P باشد. برای سادهسازی، اگر ما فرض کنیم که P دارای بار «مثبت» باشد. برای مثال، اگر یک میوه خوشمزه باشد، یک دارایی مثبت است. سپس این خوشایند است که آن را بخوریم. بنابر این، خوردن خوشایند آن، یک ارزش و دارایی مثبت است.
اصل دوم، مضاف بر مجموعهای از یک چارچوب و اصول برای P. اگر مخالف چیزی مثبت باشد سپس آن «چیز» باید منفی باشد. از این رو، گودل جهان را به یک سیاه و سفید بخش میکند: یا چیزی خوب است و یا بد. برای مثال، اگر سلامتی خوب باشد، سپس مریضی ضرورتاً چیزی بد است.
با این دو شرط، گودل اولین قضیه خود را بخش میکند: اگر φ یک دارایی و مشخصهی مثبت باشد سپس اینجا احتمالی به میان میاید که یک x با دارایی φ وجود دارد. علاوه بر ان، نشان میدهد که احتمالی برای وجود چیزی مثبت نیز وجود دارد.
در آن اکنون، ریاضیدانها برای نخستین بار تعریفی از موجودی قدسی به دست میدهند: x چیزی الهی است اگر تمام وجوه ویژگیهای مثبت φ را داشته باشد. دومین اصل متضمن آن است که تعریف خدا در این راه نمیتواند دارایی شخصیت و ویژگیهای منفی باشد (به عبارتی، میتواند زایای یک تناقض باشد).
اصل سوم، الوهیت را دارای منشی مثبت افراز میکند. این نکته حقیقتاً قابل بحث نیست چرا که الوهیت ترکیبیاست از تمام مشخصههای مثبت.
قضیهی دوم اکنون کمی بیشتر محکمتر به نظر میآید: با ترکیب اصل سوم (مثبت بودن الوهیت) و قضیهی اوّل ( احتمال وجود چیزی مثبت) که هستومند x را میتواند به عنوان وجود قدسی در نظر آورد.
اکنون هدف گودل نشان میدهد که دنبال کردن چنین رویهای، وجود خدا را ضرورتاً در چارچوب آنچه که فرض کرده، انکار ناشدنی میکند. او در تعریف دوم «وجود» φ از شئ x را بیان میکند، که در آن، این ویژگی تمامی ویژگیهای دیگر را تعیین میکند. یک مثال واضح: اگر چیزی شبیه توله سگ این ویژگی را داشته باشد، لزوماً زیبا، کرکی و چلمن است.
اصل چهارم در ابتدا خیلی هیجان انگیز به نظر نمیرسد. امّا به سادگی میگوید که اگر چیزی مثبت است، پس همیشه مثبت است – بدون توجه به زمان، موقعیت یا مکان آن. به عنوان مثال، توله سگ مانند وجود داشتن و طعمِ خوش، همیشه مثبت است، چه در روز و چه در شبی در هایدلبرگ آلمان یا بوئنوس آیرس!
بیشتر بخوانید: اسرار پیدایش زمین با مطالعهی شهاب سنگ مریخی کهنسال فاش شد!
خوب تمام اینها به چه معناییست؟
با این اوصاف اکنون گودل میتواند قضیه سوم را فرمولبندی کند: اگر هستومند x الهی باشد، الوهیّت ویژگی بنیادین آن است. خب، این منطقی است؛ زیرا اگر چیزی الهی باشد، دارای تمام ویژگی های مثبت است – و بنابراین ویژگی های x نیز ثابت خواهد بود.
وهلهی بعدی به وجود یک موجود ویژه مربوط میشود. به فرض، اگر در جایی حداقل یکی از هستومندهایی نظیر Y دارای ویژگی φ باشد که خاصیت اساسی x نیز هست، آنگاه x نیز وجود دارد. یعنی اگر آن، چیزی شبیه به توله سگ است، پس تولهها نیز باید وجود داشته باشند.
طبق اصل پنجم، وجود داشتن یک ویژگی مثبت است. گمان کنم، اکثر مردم نیز با آن موافق باشند. بنابراین، با چنین فرضی میتوان نتیجه گرفت که خدا وجود دارد زیرا این هستومند دارای هر ویژگی مثبتی است که وجود دارد.
جمعبندی تمام آنچه که گودل می گوید!
همانطور که مشخص است، استنتاجهای منطقی گودل همگی درست هستند – حتّی رایانهها نیز آن را اثبات کردهاند. با این حال، این استنباطهای او عاری نقد و نقصان نیستند علاوه بر این اصول، که البته میتوان آنها را زیر سوال برد (چرا یک جهان باید به «نیک» و «بد» تقسیم شود؟)، گودل جزئیات بیشتری درباره چیستی ویژگی مثبت ارائه نمیکند! بدیهی است که با استفاده از تعاریف و بدیهیات، میتوان مجموعه P را به صورت ریاضی توصیف کرد:
- اگر ویژگیای متعلق به مجموعه باشد، نفی آن را شامل نمیشود؛ مجموعه مستقل است.
- اینکه هستیِ یک مجموعه فقط ویژگیهای همان مجموعه را دارد که خود عنصری از مجموعه باشد. و بعد، مجموعه همیشه عناصر یکسانی نیز دارد – مستقل از موقعیّت آن! در این حالت، وضعیّت انگارهای ریاضی است که مجموعه در آن قرار دارد.
- وجود بخشی از مجموعه است.
- اگر φ بخشی از مجموعه است، پس خاصیت داشتن φ به عنوان جوهر مجموعه نیز در مجموعه موجود است. اما همه اینها تضمین نمیکند که این مجموعه منحصر به فرد است. ممکن است مجموعههای فراوانی وجود داشته باشد که الزامات آن را برآورده سازد.
به عنوان نمونه، همانطور که منطقدانان نشان دادهاند، میتوان مواردی را طرح ساخت که طبق تعریف گودل، بیش از 700 موجود الهی وجود داشته باشد که در ماهیت با هم تفاوت دارند. با این حال، این مسئله نهایی وجود اثبات خدا و یا یک (یا چند) موجود الهی دیگر را حل نمیکند. اینکه آیا ریاضیات واقعاً راه درستی برای پاسخ به این سؤال است یا نه، خود نیز محل پرسش است – حتّی اگر فکر کردن به آن بسیار هیجان انگیز نیز باشد.
بیشتر بخوانید:
- مهندسی مواد و دیانای؛ انقلابی در صنعت الکترونیک در راه است؟
- کشف یک اَبَر زمین زیستپذیر که تنها 37 سال نوری با ما فاصله دارد [+عکس]
- پیوند فوتونی راه پژوهشگران برای اینترنت کوانتومی تمام سیلیکونی
- چرا باید قید ایجاد خودآگاهی مصنوعی را بزنیم؟
شما دربارهٔ تاریخچهی اثبات خدا با ریاضیات چه فکر می کنید؟ نظرات خود را در بخش کامنتها با تکراتو در میان بگذارید.
منبع: scientificamerican