وقتی بحث از بازی در میان است سرگرمی به ذهن ما میرسد اما به حقیقت نظریه بازی ها چیست و چه کاربردی دارد ؟ در این مقاله پاسخ خود را خواهید یافت.
نظریه بازی، شاخهای از ریاضیات کاربردی است که ابزارهایی را برای تجزیه و تحلیل موقعیتهایی مانند تصمیم گیری برخی از بازیکنان فراهم میکند. این تصمیم گیریها اصولا به هم وابسته هستند. این وابستگی متقابل بین بازیکنان باعث میشود که هر کدام از آنها تا حدودی بتوانند استراتژیهای احتمالی یک بازیکن دیگر را بفهمند برای استراتژیهای خود از آن بهره ببرد.
نظریه بازی در واقع یک راه حل بوده که تصمیمات بازیکنان در یک بازی را که ممکن است علایق مشابه، مخالف یا مختلطی داشته باشند و نتایجی که ممکن است از این تصمیمات حاصل شود را توصیف میکند. اگرچه تئوری بازیها میتواند برای تجزیه و تحلیل بین یک گروه یا چندین گروه مورد استفاده قرار گیرد، اما کاربردهای آن بسیار گستردهتر از آنچه به نظر میرسد است. در ادامه با توصیف نظریه بازی ها به زبان ساده همراه ما باشید.
نظریه بازی ها چیست و چه کاربردی دارد ؟
حتما دوست دارید به طور دقیق بدانید نظریه بازی ها چیست و چه کاربردی دارد در این قسمت جواب خود را خواهید گرفت. نظریه بازیها در اصل توسط ریاضیدان آمریکایی مجارستانی الاصل جان فون نویمان و همکارش در دانشگاه پرینستون، اسکار مورگنسترن، اقتصاددان آمریکایی آلمانی الاصل، برای حل مسائل در اقتصاد ایجاد شد.
فون نویمان و مورگنسترن در کتاب خود به نام تئوری بازیها و رفتار اقتصادی در جواب نظریه بازی ها چیست و چه کاربردی دارد گفتهاند که ریاضیات توسعهیافته برای علوم فیزیکی، که کارکرد ماهیت بیعلاقهای را توصیف میکند، مدل ضعیفی برای اقتصاد است.
آنها مشاهده کردند که اقتصاد بسیار شبیه یک بازی است که در آن بازیکنان حرکات یکدیگر را پیشبینی میکنند و بنابراین اقتصاد نیاز به نوع جدیدی از ریاضیات دارد که آن را نظریه بازی نامیدند. ممکن است نام بازی بسیار برای این علم ریاضی مناسب نباشد زیرا از نظریه بازی که یک راه حل پیشرفته است برای سرگرمی یا بیهودگی مرتبط با بازیها استفاده نمیشود و در آن کاربرد چندانی ندارد.
نظریه بازی یک چارچوب نظری برای درک موقعیتهای اجتماعی در بین بازیکنان یا همان افراد رقیب است. از برخی جهات، نظریه بازی علم استراتژی یا حداقل تصمیم گیری بهینه بازیگران مستقل و رقیب در یک محیط استراتژیک است.
تئوری بازی در طیف گستردهای از موقعیتها به کار گرفته میشود که در آنها انتخاب بازیکنان برای تأثیرگذاری بر نتیجه تعامل دارند. علاوه بر آن در تأکید بر جنبههای استراتژیک تصمیمگیری، یا جنبههایی که توسط بازیکنان کنترل میشوند، این نظریه هم مکمل نظریه کلاسیک احتمالات است و هم فراتر میرود.
اگر بخواهیم چند مثال در ارتباط با کاربردهای تئوری گیم بگوییم بدین شکل هستند: تعیین اینکه چه ائتلافهای سیاسی یا گروههای تجاری احتمالاً تشکیل میشوند، قیمت بهینه برای فروش محصولات یا خدمات در مواجهه با رقابت، قدرت یک رأیدهنده یا بلوک رأیدهندگان، انتخاب برای هیئت داوران، بهترین سایت برای یک کارخانه تولیدی و رفتار حیوانات و گیاهان خاص در مبارزه آنها برای بقا.
از این نظریه حتی برای به چالش کشیدن قانونی بودن برخی از سیستمهای رای گیری استفاده شده است. اگر هر نظریهای بتواند به چنین طیف عظیمی از به اصلاح بازیها بپردازد، تعجب آور خواهد بود، و در واقع هیچ نظریه بازی واحدی وجود نخواهد داشت.
نظریههای زیادی ارائه شده که هر کدام در موقعیتهای مختلف قابل استفاده هستند. هر کدام از این نظریهها مفاهیم خاص خود را در مورد راه حلها در شرایط مختلف میدهند. ما در این قسمت تا حدودی به برسی سوال نظریه بازی ها چیست و چه کاربردی دارد پرداختیم در ادامه قصد داریم به نحوه کارکرد این نظریه بپردازیم.
نحوه کارکرد نظریه بازی ها

این بازی هویت، ترجیحات و استراتژیهای موجود بازیکنان و چگونگی تأثیر این استراتژیها بر نتیجه را مشخص میکند. نکته اصلی و قابل توجه برای اجرای این نظریه همان نتیجه است که بسته به مدل، الزامات یا مفروضات مختلف دیگری ممکن است متفاوت باشد.
نظریه بازیها کاربردهای گستردهای دارد، از جمله در زمینه روانشناسی، زیست شناسی تکاملی، جنگ، سیاست، اقتصاد و تجارت. با وجود پیشرفتهای فراوان، نظریه بازیها یک علم نو و در حال توسعه بوده که هنوز به شکل خاصی بین افراد جا نیوفتاده است.
بر اساس تئوری بازی ها، اقدامات و انتخابهای همه شرکت کنندگان بر نتیجه هر یک تأثیر می گذارد. فرض بر این است که بازیکنان درون بازی منطقی هستند و تلاش خواهند کرد تا بازده خود را در بازی به حداکثر برسانند.
هر زمان که موقعیتی به همراه دو یا چند بازیکن داشتیم و شرایط شامل پیامدهای قابل سنجش بود، میتوانیم از تئوری بازی برای کمک به تعیین محتملترین نتایج استفاده کنیم. حالا که به طور کامل به سوال نظریه بازی ها چیست و چه کاربردی دارد پاسخ داده شد قصد داریم به برسی کاربردهای تئوری بازی ها بپردازیم اما پیش از هر چیزی اجازه دهید شما را با برخی اصطلاحات آشنا کنیم.
ابتدا باید برای شما سوال باشد که منظور از بازی چیست؟ همانطور که اعلام کردیم این بحث بازی تئوری در جهت سرگرمی و اوقات فراغت نیست. اصطلاح بازی در واقع همان مجموعه شرایطی است که نتیجه آن به اقدامات دو یا چند تصمیم گیرنده یا همان بازیکن بستگی دارد.
اصطلاح بازیکن در واقع به معنی یک تصمیم گیرنده استراتژیک بوده که تمام تصمیمات خود را در چارچوب بازی میگیرد. اصطلاح استراتژی به معنای یک برنامه کامل عملی بوده که یک بازیکن با توجه به مجموعه شرایطی که ممکن است در بازی ایجاد شود، انجام خواهد داد.
اصطلاح هزینه یا منفعت همان مبلغی است که یک بازیکن از جهت رسیدن به یک نتیجه خاص مورد نظر دریافت میکند. هزینه میتواند به هر شکل قابل اندازه گیری باشد، از دلار گرفته تا ابزار مفید.
اصطلاح مجموعه اطلاعات در واقع به معنای اطلاعات موجود در یک نقطه معین از بازی است. مجموعه اطلاعات معمولاً زمانی به کار میرود که بازی دارای یک جزء متوالی باشد. اصطلاح تعادل به معنای نقطهای در بازی است که هر دو بازیکن تصمیمات خود را گرفتهاند و به نتیجه میرسند.
آشنایی با توکنهای NFT:
تعادل نش

تعادل نش راه حلی از تئوری بازی بوده که پس از دستیابی به آن بدین معنی است که هیچ بازیکنی نمیتواند با تغییر تصمیمات به طور یکجانبه، سود خود را افزایش دهد. همچنین میتوان آن را مفهومی با عنوان تصمیم گیری بدون پشیمانی در نظر گرفت، به این معنا که به محض تصمیم گیری، بازیکن در مورد تصمیمات با توجه به عواقب آن پشیمان نخواهد شد.
در بیشتر موارد تعادل نش در طول زمان به دست می آید و به طور کلی در یک بازی بیش از یک تعادل نش وجود دارد. با این حال، این شرایط معمولا در بازیهایی با عناصر پیچیدهتر از دو انتخاب توسط دو بازیکن رخ میدهد.
در بازیهای همزمان که در طول زمان تکرار میشوند و نیاز به هماهنگی دارد، پس از مدتی آزمون و خطا به یکی از این تعادلهای چندگانه می رسند. این سناریوی انتخابهای مشابه و بدون پشیمانی، اغلب در دنیای تجارت انجام می شود. برای مثال، زمانی که دو شرکت در حال تعیین قیمت بلیط هواپیما هستند.
اثر نظریه بازی بر اقتصاد و کسب و کار
یکی از کاربردهای تئوری بازی ها این است که کمک شایانی به حل مسائل اقتصادی و تجارتی میکند. گیم تئوری با پرداختن به مسائل مهم در مدلهای اقتصادی ریاضی، انقلابی در اقتصاد به وجود آورده است. برای مثال، اقتصاد نئوکلاسیک برای درک پیشبینی کارآفرینانه تلاش میکرد و نمیتوانست رقابت ناقص را مدیریت کند. تئوری بازی توجه را از تعادل حالت پایدار به سمت فرآیند بازار معطوف کرده است.
در تجارت، نظریه بازی برای مدل سازی رفتارهای رقابتی بین عوامل اقتصادی سودمند است. کسب و کارها اغلب چندین انتخاب استراتژیک دارند که بر توانایی آنها برای تحقق سود اقتصادی تأثیر میگذارد. برای مثال، کسبوکارها ممکن است با معضلاتی مانند بازنشستگی محصولات موجود یا توسعه محصولات جدید، کاهش قیمتها نسبت به رقبا، یا به کارگیری استراتژیهای بازاریابی جدید مواجه شوند.
اقتصاددانان اغلب از نظریه بازی برای درک رفتار شرکتهای انحصاری استفاده میکنند. این نظریه بسیار به پیش بینی نتایج احتمالی رفتارهای خاصی مانند تثبیت قیمت و تبانی شرکتها کمک میکند. تا حدودی شما پاسخ به سوال نظریه بازی ها چیست و چه کاربردی دارد را یافتید در ادامه با طبقه بندی بازیها همراه ما باشید.
با بازیهای متاورسی آشنا شوید:
آموزش بازی رولرکوین (Rollercoin)
طبقه بندی بازی ها

بازیها را میتوان بر اساس ویژگیهای مهمی دستهبندی کرد که بارزترین این ویژگیها تعداد بازیکنان است. بنابراین، یک بازی را میتوان به عنوان یک بازی یک نفره، دو نفره یا n-نفره در نظر گرفت. بازیهای هر دسته ویژگیهای مختلف خود را دارند. علاوه بر این، یک بازیکن لزوما یک فرد نیست، ممکن است یک ملت، یک شرکت یا تیمی متشکل از افراد زیاد با علایق مشترک باشد.
در بازیهایی که اطلاعات کامل در دسترس است، مانند شطرنج، هر بازیکن همیشه همه چیز را در مورد بازی میداند. از سوی دیگر، پوکر نمونهای از یک بازی اطلاعات ناقص است زیرا بازیکنان نظری درباره تمام کارتهای حریف خود ندارند.
میزان تطابق یا تضاد اهداف بازیکنان مبنای دیگری برای طبقه بندی بازیها است. بازیهای مجموع ثابت، به بازیهایی گفته میشود که تعداد بازیکنان یا شرایط آن ثابت باشد، به این بازیها، بازیهای رقابتی نیز میگویند. به عنوان مثال، پوکر یک بازی با جمع ثابت است، زیرا پول ترکیبی بازیکنان ثابت میماند، اگرچه توزیع آن در طول بازی تغییر پیدا میکند.
بازیکنان در بازیهای جمع ثابت علایق کاملاً متضاد دارند، در حالی که در بازی مجموع متغیر همه ممکن است برنده یا بازنده باشند. به عنوان مثال، در یک اختلاف مدیریت کار، دو طرف مطمئناً دارای برخی از منافع متضاد هستند، اما اگر از اعتصاب جلوگیری شود، هر دو سود خواهند برد.
بازیهای مجموع متغیر را میتوان به صورت مشارکتی یا غیرهمکارانه متمایز کرد. در بازیهای تعاونی، بازیکنان میتوانند با هم ارتباط برقرار کنند و مهمتر از همه، توافقهای الزامی را امضا کنند. در بازیهای غیرهمکارانه، بازیکنان ممکن است با هم ارتباط برقرار کنند، اما نمیتوانند توافقهای الزامی مانند قرارداد قابل اجرا ببندند.
یک فروشنده خودرو و یک مشتری بالقوه در صورت توافق بر سر قیمت و امضای قرارداد، درگیر یک بازی تعاونی خواهند شد. با این حال، تلاشی که آنها برای رسیدن به این نقطه انجام میدهند، غیرهمکارانه خواهد بود. به طور مشابه، هنگامی که مردم به طور مستقل در یک حراج پیشنهاد میدهند، آنها یک بازی غیرهمکارانه انجام میدهند.
در نهایت، زمانی گفته میشود که یک بازی محدود است که هر بازیکن تعداد محدودی گزینه داشته باشد، تعداد بازیکنان محدود باشد و بازی نتواند به طور نامحدود ادامه یابد. مثالی برای آن شطرنج و پوکر است.
فرم معمولی (استراتژیک) در درجه اول برای توصیف بازیهای دو نفره استفاده میشود. در این شکل یک بازی با یک ماتریس نمایش داده میشود که در آن هر ردیف استراتژی یک بازیکن و هر ستون استراتژی بازیکن دیگر را توصیف میکند. ورودی ماتریس در تقاطع هر سطر و ستون نتیجه انتخاب استراتژی مربوطه را به هر بازیکن نشان میدهد. بازده هر بازیکن مرتبط با این نتیجه، مبنایی برای تعیین تعادل استراتژیها است.
اگرچه انواع مختلفی از تئوریهای بازی وجود دارد (به عنوان مثال، متقارن/نامتقارن، همزمان/متوالی، و غیره)، نظریههای بازی تعاونی و غیرهمکارانه رایجترین آنها هستند. تئوری بازیهای تعاونی به نحوه تعامل ائتلافها یا گروههای تعاونی در زمانی میپردازد که فقط بازده آن مشخص است.
نظریه بازیهای غیرهمکارانه به نحوه برخورد عوامل اقتصادی منطقی با یکدیگر برای رسیدن به اهداف خود میپردازد. متداولترین بازی غیرهمکارانه، بازی استراتژیک بوده که در آن فقط استراتژیهای موجود و نتایج حاصل از انتخابها فهرست شده است. یک مثال ساده از یک بازی غیرهمکارانه در دنیای واقعی، سنگ-کاغذ-قیچی است.
فرم معمولی (استراتژیک) در درجه اول برای توصیف بازیهای دو نفره استفاده میشود. در این شکل یک بازی با یک ماتریس بازده نمایش داده میشود که در آن هر ردیف استراتژی یک بازیکن و هر ستون استراتژی بازیکن دیگر را توصیف میکند. ورودی ماتریس در تقاطع هر سطر و ستون نتیجه انتخاب استراتژی مربوطه را به هر بازیکن نشان میدهد. بازده هر بازیکن مرتبط با این نتیجه، مبنایی برای تعیین تعادل استراتژی است.
با بازیهای متاورسی آشنا شوید:
بازی های تک نفره

بازیهای تک نفره به اصطلاح به عنوان بازی علیه طبیعت نیز شناخته میشوند. بدون هیچ حریفی، بازیکن فقط باید گزینههای موجود را فهرست کرده و سپس بهترین نتیجه را انتخاب کند. وقتی شانس در میان باشد، ممکن است بازی پیچیدهتر به نظر برسد، اما در اصل تصمیم نسبتاً ساده است.
به عنوان مثال، فردی که تصمیم میگیرد چتر با خود حمل کند، هزینهها و مزایای حمل یا عدم حمل آن را میسنجد. در حالی که این شخص ممکن است تصمیم اشتباهی بگیرد، اما یک مخالف و آگاه واقعی وجود ندارد.
یعنی طبیعت و جهان کاملاً نسبت به تصمیم بازیکن بی تفاوت فرض میشوند و فرد میتواند تصمیم خود را بر اساس احتمالات ساده بگیرد. بازیهای تک نفره برای نظریه پردازان بازیها جذابیت چندانی ندارد. پاسخ سوال نظریه بازی ها چیست و چه کاربردی دارد باید در حال حاضر به خوبی برای شما قابل لمس باشد.
بازی های اطلاعات کامل
سادهترین بازی از هر نظری، یک بازی دو نفره با جمع ثابت و اطلاعات کامل است. نمونههایی از این گونه بازیها شامل شطرنج، چکرز و بازی ژاپنی گو است. در سال 1912، ارنست زرملو، ریاضیدان آلمانی ثابت کرد که چنین بازیهایی کاملاً قابل تشخیص هستند.
با استفاده از تمام اطلاعات موجود، بازیکنان میتوانند استراتژیهایی را استنباط کنند که بهترین نتیجه را برای آنها ایجاد کند. این موضوع باعث میشود نتیجه از پیش تعیین شده شود. به عنوان مثال در بازی شطرنج 3 حالت ممکن است بنا به تصمیمها و شرایط اتفاق بیوفتد: اول اینکه سفید ببرد دوم اینکه سیاه ببرد و سوم اینکه هر دو مساوی شوند. حالا سعی کنید این شرایط را در زندگی عادی خود تطبیق دهید.
The Prisoner’s Dilemma (دو راهی زندانی)
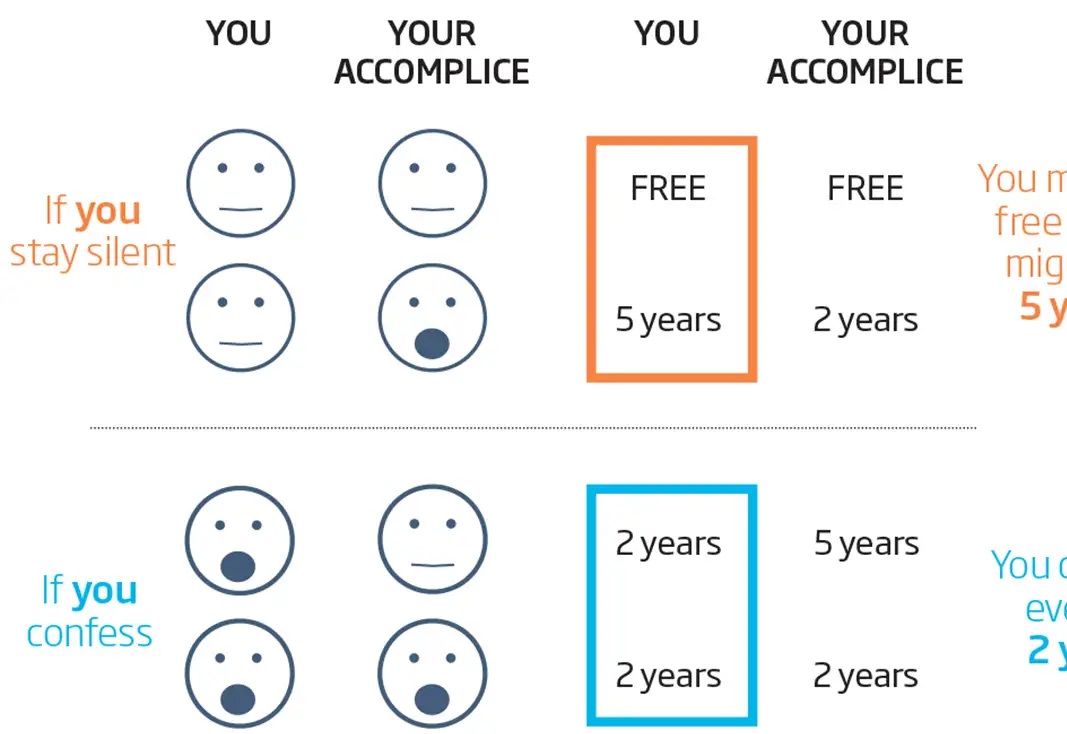
برای نشان دادن انواع مشکلاتی که در بازیهای مجموع متغیر غیرهمکارانه بین دو نفر به وجود میآید، معمای زندانی مشهور (PD) را در نظر بگیرید که در اصل توسط ریاضیدان آمریکایی آلبرت دبلیو. تاکر فرموله شده است.
دوراهی زندانی شناخته شده ترین نمونه نظریه بازی است. به این مثال که دو جنایتکار به دلیل یک جنایت دستگیر شدند، توجه کنید. دادستانها هیچ مدرک محکمی برای محکومیت آنها ندارند. با این حال، مقامات برای گرفتن اعتراف، زندانیان را از سلولهای انفرادی خود خارج کرده و هر یک را در اتاقهای جداگانه مورد بازجویی قرار میدهند.
هیچ یک از زندانیان ابزاری برای برقراری ارتباط با یکدیگر ندارند. مقامات چهار معامله ارائه میدهند که اغلب به صورت یک جعبه 2×2 نمایش داده می شود. اگر هر دو اعتراف کنند، هر کدام به پنج سال زندان محکوم خواهند شد.
اگر زندانی 1 اعتراف کند، اما زندانی 2 اعتراف نکند، زندانی 1 سه سال و زندانی 2 حدود 9 سال محکوم خواهند شد. اگر زندانی 2 اعتراف کند، اما زندانی 1 اعتراف نکند، زندانی 1 حدود 10 سال و زندانی 2 دو سال محکوم خواهند شد. اگر هیچ کدام اعتراف نکنند، هر کدام دو سال به زندان محکوم خواهند شد.
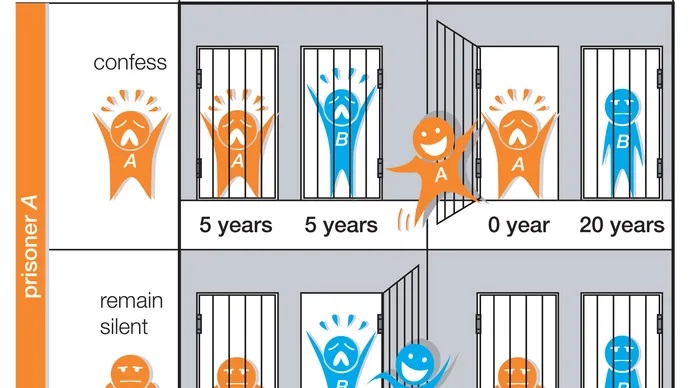
مطلوب ترین راهبرد اعتراف نکردن است. با این حال، هیچ یک از استراتژی دیگری آگاه نیستند و بدون اطمینان از اینکه یکی اعتراف نخواهد کرد، هر دو احتمالاً اعتراف خواهند کرد و به پنج سال زندان محکوم خواهند شد.
تعادل نش نشان میدهد که در دوراهی یک زندانی، هر دو بازیکن حرکتی را انجام میدهند که برای آنها بهترین است اما برای آنها در مجموع بد تمام خواهد شد. نکته جالب PD این است که وقتی هر یک از دو یا چند طرف خودخواهانه عمل کنند و با دیگری همکاری نکنند، بدتر از زمانی است که غیر خودخواهانه عمل کرده و با هم همکاری کنند.
تعبیر تیت فور تت یا همان این به اون در خودمان به عنوان یک استراتژی برای بهتر کردن شرایط یک زندانی تعیین شده است. تیت فور تت توسط آناتول راپوپورت معرفی شد، او یک استراتژی را ایجاد کرد که در آن هر یک از شرکتکنندگان در یک دوراهی، مسیری را دنبال کنند که مطابق با حرف قبلی حریف است. به عنوان مثال، اگر یک بازیکن تحریک شود، متعاقباً با تلافی پاسخ میدهد. در صورت عدم تحریک، بازیکن همکاری میکند.
موقعیتهای واقعی زندگی با ویژگیهای مشابه با دوراهی زندانی اغلب مشاهده شده است. برای مثال، دو مغازه دار که درگیر جنگ قیمت هستند ممکن است درگیر یک PD شوند. هر مغازهداری میداند که اگر قیمتهای کمتری نسبت به رقیب خود داشته باشد، مشتریان رقیب خود را جذب میکند و در نتیجه سود خود را افزایش میدهد.
بنابراین هر کدام تصمیم میگیرند قیمتهای خود را پایین بیاورند، در نتیجه هیچ یک مشتری به دست نیاورده و هر دو سود کمتری کسب میکنند. به طور مشابه، کشورهایی که در یک مسابقه تسلیحاتی با هم رقابت میکنند و کشاورزانی که تولید محصول را افزایش میدهند نیز میتوانند به عنوان مظاهر PD دیده شوند.
وقتی دو کشور در تلاش برای دستیابی به برتری نظامی به خرید تسلیحات بیشتر ادامه میدهند، هیچ کدام مزیتی به دست نمیآورند و هر دو فقیرتر از زمانی هستند که شروع کردند. یک کشاورز تنها میتواند با افزایش تولید، سود خود را افزایش دهد، اما زمانی که همه کشاورزان تولید خود را افزایش دهند، مازاد بازار به وجود میآید و سود کمتری برای همه به همراه خواهد داشت.
بهترین سرمایه گذاریها در متاورس:
بهترین پروژه های متاورس برای خرید و سرمایه گذاری
آینده متاورس و پیش بینی قیمت ارزهای متاورسی
Dictator Game (بازی دیکتاتور)
Dictator Game یک بازی ساده است که در آن بازیکن A باید تصمیم بگیرد که چگونه یک جایزه نقدی را با بازیکن B، که هیچ دخالتی در تصمیم بازیکن A ندارد، تقسیم کند. اگرچه این به خودی خود یک استراتژی تئوری بازی نیست، اما بینش جالبی را در مورد رفتار افراد ارائه می دهد. آزمایشها نشان میدهد که حدود 50٪ تمام پول را برای خود نگه میدارند، 5٪ آن را به طور مساوی تقسیم میکنند و 45٪ دیگر سهم کمتری به شرکتکننده دیگر میدهند.
بازی دیکتاتور ارتباط نزدیکی با بازی اولتیماتوم دارد که در آن به بازیکن A مقدار مشخصی پول داده میشود که بخشی از آن باید به بازیکن B داده شود. بازیکن B می تواند مبلغ داده شده را بپذیرد یا رد کند. نتیجه این است که اگر بازیکن دوم مبلغ پیشنهادی را رد کند، هر دو بازیکن A و B چیزی دریافت نخواهند کرد. بازیهای دیکتاتور و اولتیماتوم درسهای مهمی برای مسائلی مانند کمکهای خیریه و بشردوستی دارد.
Volunteer’s Dilemma (معمای داوطلب)

در بازی معمای داوطلب، یک نفر باید یک کار یا کاری را برای منافع عمومی انجام دهد. بدترین نتیجه ممکن در صورتی محقق میشود که کسی داوطلب برای این کار نشود. به عنوان مثال، شرکتی را در نظر بگیرید که در آن صورتهای مالی شرکت پر از اشتباهات است، هرچند مدیریت عامل از آن بیخبر باشد.
قطعا برخی از کارمندان در بخش حسابداری از این فاجعه اطلاع دارند، اما در گفتن به مدیریت عامل تردید دارند، زیرا این امر منجر به اخراج کارکنان دخیل در این اشتباه شده و به احتمال زیاد تحت پیگرد قانونی قرار میگیرند.
برچسب زدن به عنوان یک افشاگر نیز ممکن است عواقبی داشته باشد. اما اگر هیچ کس داوطلب نشود، این اشتباه در مقیاس بزرگ ممکن است منجر به ورشکستگی نهایی شرکت و از دست دادن شغل همه شود.
محدودیتهای تئوری بازی
بزرگترین مشکل گیم تئوری این است که مانند بسیاری از مدلهای اقتصادی دیگر، بر این فرض تکیه میکند که مردم بازیگرانی منطقی هستند که تنها به نفع شخصی و حداکثر سودمندی خود فکر میکنند.
البته که ما موجوداتی اجتماعی هستیم و اغلب با خودمان و اجتماعها کاری کرده و به رفاه دیگران اهمیت میدهیم. نظریه بازی نمیتواند این واقعیت را توضیح دهد که در برخی موقعیتها ممکن است ما در تعادل نش قرار بگیریم، و در برخی مواقع نه، این موضوع نیز بستگی به شرایط و افراد خواهد داشت.
چه بازیهایی در تئوری بازیها استفاده می شود ؟
نظریه بازی همانطور که گفتیم یک شاخهای از ریاضیات بوده که در زندگی عادی هم میتواند بسیار موثر باشد. به این علم نظریه بازی میگوییم زیرا این نظریه سعی میکند اقدامات استراتژیک دو یا چند به اصطلاح بازیکن را در یک موقعیت معین حاوی قوانین و نتایج تعیین شده درک کند. در حالی که در چندین رشته مورد استفاده قرار میگیرد، نظریه بازی بیشتر به عنوان ابزاری در مطالعه تجارت و اقتصاد استفاده میشود.
بازیها ممکن است شامل نحوه واکنش دو شرکت رقیب به کاهش قیمت توسط دیگری باشد، یا اینکه معاملهگران در یک بازار سهام چگونه ممکن است به تغییرات قیمت واکنش نشان دهند. از نظر تئوریک، این بازیها را میتوان به عنوان دوراهی زندانی، بازی دیکتاتور و غیره طبقهبندی کرد.
مطالب بیشتر در تکراتو:
- بهترین بازی های متاورس برای کسب درآمد
- آموزش سرمایه گذاری در متاورس
- متاورس چیست و چگونه وارد Metaverse شویم؟
- زمین مجازی چیست و سرمایه گذاری در متاورس چگونه است؟
- بهترین پروژه ها و ارزهای وب 3 (Web 3.0)
- وب 3 یا نسل سوم وب چیست ؟
.
منبع: investopedia
نظر شما در خصوص نظریه بازی ها چیست ؟ نظرات خود را در بخش کامنت ها با تکراتو در میان بگذارید.





